Lehrstuhl für Informatik 12 (Hardware-Software-Co-Design)
Herzlich willkommen!
Forschungsschwerpunkt des Lehrstuhls Hardware-Software-Co-Design ist der systematische Entwurf (CAD) eingebetteter Hardware/Software-Systeme.
Die bekanntesten Beispiele für solche Systeme sind wohl Smartphones, aber auch andere Geräte des täglichen Lebens. Beginnend vom Radiowecker, über den Kaffeevollautomaten und dem Auto sind wir von einer Vielzahl solcher Computersysteme umgeben ohne es bewusst wahr zunehmen. Sie erfüllen alle für sich einen speziellen Zweck oder sind auf besondere Bereiche optimiert. Beispielsweise soll ein Handy möglichst performant sein, dabei aber möglichst wenig Strom verbrauchen.
Wie man diese Systeme entwickelt, welche Randbedingungen man dabei beachten muss, welche Technologien, Programmiersprachen (SystemC, C++, Simulink, usw.) und Compiler man verwenden und entwickeln/anpassen kann, das sind die Fragen, die uns interessieren.
Heutige Fertigungstechnologien von elektronischen Schaltungen ermöglichen eine Vielzahl von Architekturen, die in eingebetteten Systemen eingesetzt werden. Moderne Mobiltelefone enthalten bereits vier Prozessorkerne und mehr. In aktuellen Grafikkarten arbeiten mehrere tausend Recheneinheiten parallel. Diese Art von Systemen, die mehrere heterogene Prozessor- oder Recheneinheiten auf einem Chip beinhalten, bezeichnet man als Multi-Procesessor-Systems-on-Chip (MPSoC).
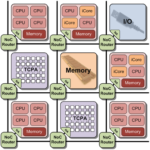
Um diese Architekturen optimal ausnutzen zu können, sind spezielle Compiler nötig. Der Compiler übersetzt den vom Menschen lesbaren Programmcode einer Programmiersprache (z.B. C++) in einen vom Zielsystem ausführbaren Maschinencode (z.B. für die optimale Ausnutzung der hohen Parallelität einer Grafikkarte).
Im Gebiet Reconfigurable Computing forschen wir an der Optimierung und Weiterentwicklung solcher Systeme, um beispielsweise Zuverlässigkeit, Sicherheit und Verfügbarkeit von nanoelektrischen Schaltungen zu erhöhen.

Hierfür wird das Potential von FPGAs ausgenutzt. Diese Chips sind bei der Herstellung nicht fest auf eine Anwendung spezialisiert, sondern neu programmierbar. Bei der Realisierung eines eingebetteten Systems kann man entscheiden, welche Teile der Funktionalität in Hardware und welche in Software realisiert werden sollen, es erfolgt ein Hardware-Software-Co-Design-Entwurf. Wir untersuchen, wie Bereiche dieser FPGAs während der Laufzeit ausgetauscht werden können, ohne den Betrieb zu stören. Eine mögliche Anwendung wäre, dass ein Bauteil im Auto die Funktionalität eines anderen Bauteils übernimmt, wenn dieses ausfällt (die Steuerung des Blinkers übernimmt z.B. auch die Steuerung des ABS).
Der Schwerpunkt der effizienten Algorithmen und kombinatorischen Optimierung ist die Erforschung von effizienten Algorithmen (Programmabläufe) für lokale und globale Such- und Mehrzieloptimierungsverfahren und deren Anwendungen. Ein gutes Beispiel ist die Raumplanung der Technischen Fakultät der Universität. Für die angebotenen Lehrveranstaltungen müssen Räume gefunden werden, die die erforderlichen Parameter erfüllen, wie z.B. Raumgröße, Verfügbarkeit und Uhrzeit. Das an unserem Lehrstuhl entwickelte Verfahren liefert in kürzester Zeit ein optimales Ergebnis.







